DiGS: Divergence guided shape implicit neural representation for unoriented point clouds

CVPR 2022

Yizhak Ben-Shabat (Itzik)
Yizhak Ben-Shabat
(Itzik)*1,2,3 Chamin Hewa Koneputugodage
Chamin Hewa
Koneputugodage*1,3 Stephen Gould
Stephen Gould 1,3
 
1The Australian National University   2Technion  3Australian Centre for Robotic Vision
*Equal Contribution
Paper Paper arxiv Arxiv Code Code Video Video Video Podcast

Results on the Surface Reconstruction Benchmark. DiGS, which does not use normals, does as well as methods that use normals (SIREN shown here) and much better than methods that do not (IGR wo n shown here).

Results on the scene from SIREN's paper. To be able to fit complex scenes, normal supervision is essential for INR based methods. Here we demonstate that our method is able to still work well without normals, while SoTA method SIREN has a lot of ghost geometry in the absence of normal supervision.

Abstract

Shape implicit neural representations (INRs) have recently shown to be effective in shape analysis and reconstruction tasks. Existing INRs require point coordinates to learn the implicit level sets of the shape. When a normal vector is available for each point, a higher fidelity representation can be learned, however normal vectors are often not provided as raw data. Furthermore, the method's initialization has been shown to play a crucial role for surface reconstruction.
In this paper, we propose a divergence guided shape representation learning approach that does not require normal vectors as input. We show that incorporating a soft constraint on the divergence of the distance function favours smooth solutions that reliably orients gradients to match the unknown normal at each point, in some cases even better than approaches that use ground truth normal vectors directly. Additionally, we introduce a novel geometric initialization method for sinusoidal INRs that further improves convergence to the desired solution. We evaluate the effectiveness of our approach on the task of surface reconstruction and shape space learning and show SOTA performance compared to other unoriented methods.

Video

Divergence Guided Shape INRs

We tackle the problem of point cloud reconstruction in the absence of normal information. We use a smooth-to-sharp approach that keeps the gradient vector field stay highly consistent during training. It has four stages (see Training Procedure video below)

  • Geometric Initialization
  • High Divergence Phase
  • Annealing Divergence Phase
  • Low Divergence Phase
In order to implement this training procedure, we have two main contributions: our Geometric Initialisation and our Divergence Loss.

Training Procedure

Divergence Loss

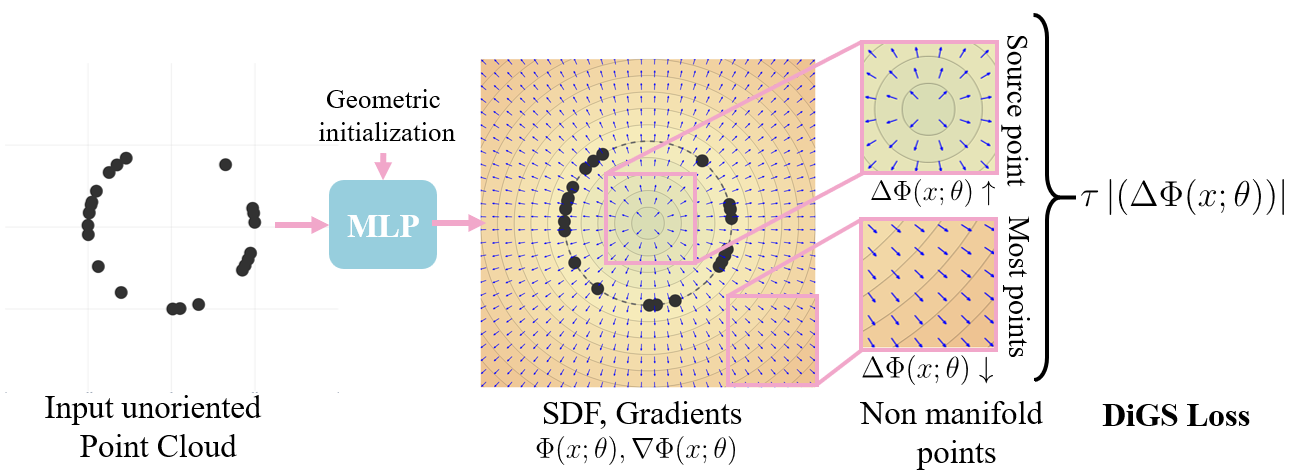
teaser

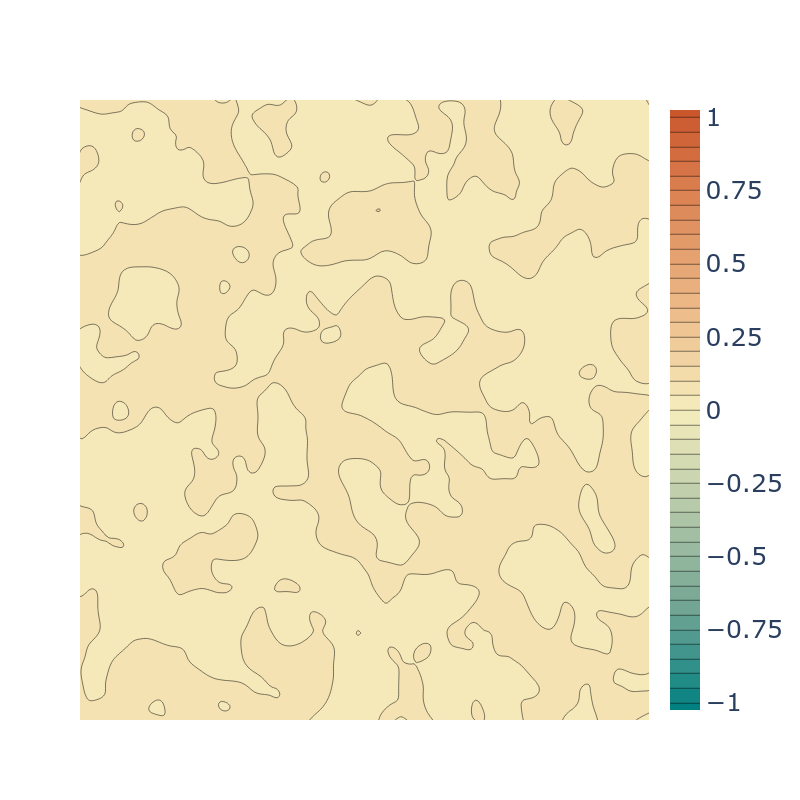
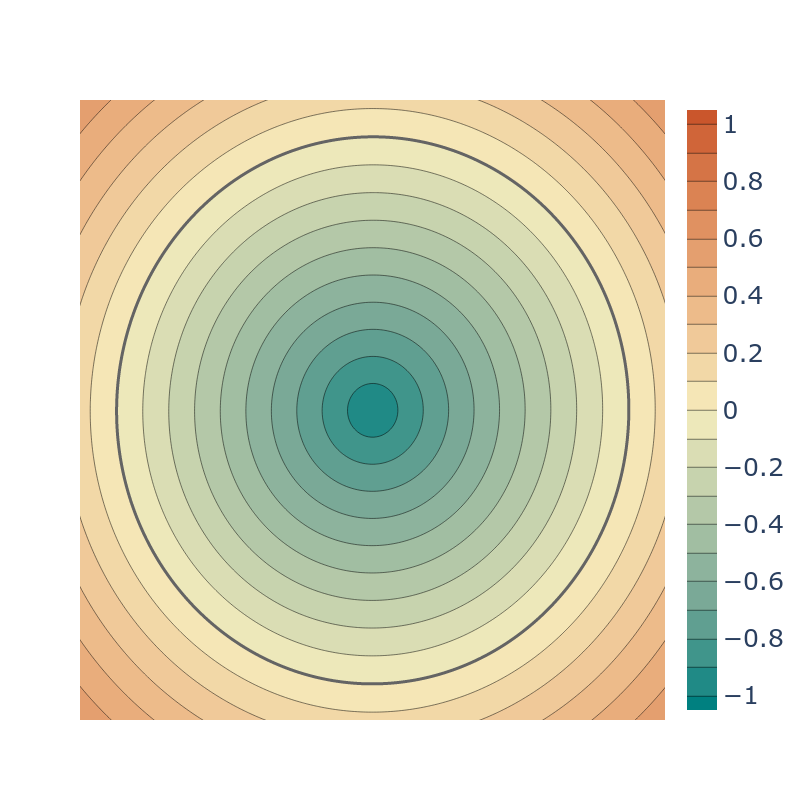
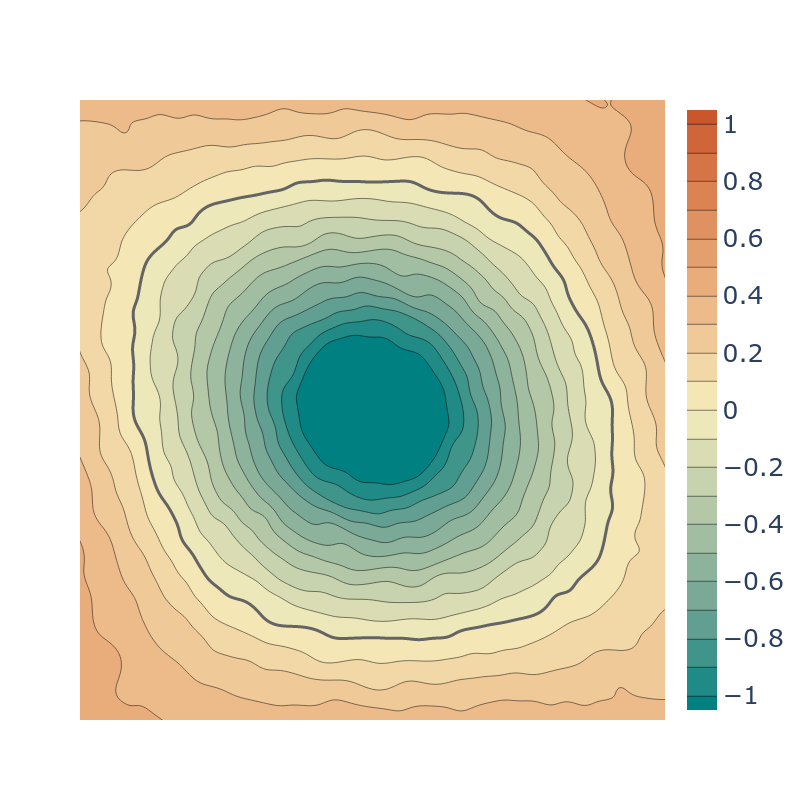
Motivated by the observation that ground truth signed distance functions have low divergence nearly everywhere (see above figure), we incorporate this geometric prior. Specifically we use it as a soft constraint during training, which keeps our gradient vector field stay highly consistent, and anneal it as training progresses. We show that this loss is essentially a regularization term, minimising the Dirichlet Energy or "complexity" of the learnt function. We also demonstrate in toy examples that this is more effective that just the Eikonal term in both reducing the Dirichlet Energy and in obeying the Eikonal constraint.

Geometric Initialisation

siren
SIREN
geometric-sine
Our Geometric Sine
mfgi
Our MFGI

We also provide two geometric initializations for SIRENs. Similar to previous geometric initializations (e.g. SAL) we introduce a spherical initialization that works for SIRENs. Such initializations initialise the function to have an SDF for a sphere, thus biasing it to have a good eikonal loss, and to have positive SDF away from the object while negative SDF around the center of the object's bounding box.
However this initialization biases the network to learn lower frequency solutions, so we also introduce a modification, multi-frequency geometric initialization (MFGI), which keeps the model's ability to have high frequencies while maintaining the previous properties.


Additional Results

A much more challenging task than scene reconstruction is the shapespace task, where a single network learns to represent a space of related objects by training to reconstruct on a subset of such objects' point clouds (the pink frames). When using normals (shown here), our method is able to maintain a more consistent shape (e.g. minimal loss of limb structure) and less ghost geometry that other methods, but oversmooths fine detail (e.g. the face). When not using normals, our method is still able to learn, while other methods are not able to.

Acknowledgements

This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 893465

BibTeX

@inproceedings{ben2022digs,
    title={DiGS: Divergence guided shape implicit neural representation for unoriented point clouds},
    author={Ben-Shabat, Yizhak and Hewa Koneputugodage, Chamin and Gould, Stephen},
    booktitle={Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition},
    pages={19323--19332},
    year={2022}
  }